Algebra and Functions
A
Indices and Surds
Let's start by having a look at a couple of ways to write numbers. Firstly we shall look at indices. We use indices to show repeated multiplication. Then we'll move on to surds, which is when we use square-root symbols and the like.
Laws of Indices
2 x 2 x 2 x 2 x 2 can be shortened to 25 as there are five twos multiplied together.
We shall now look at some rules for working with indices.
23 x 25 = (2 x 2 x 2) x (2 x 2 x 2 x 2 x 2) = 28.
This gives us our first rule: when you multiply two numbers with the same base (here 2), you simply add the indices.
This is a bit boring to type, so have a watch of this clip I made.
Rationalising Denominators
Some fractions are just plain ugly. Have a look at this clip to see what we can do to fix this.
If you prefer a Welsh accent, look at this clip
Quadratics
Quadratic functions are very important. They crop up everywhere. We shall see more of these as we go through the course but you will see them an awful lot in mechanics lessons.
Quadratic Graphs
We will start by looking at what a graph of a quadratic function looks like.
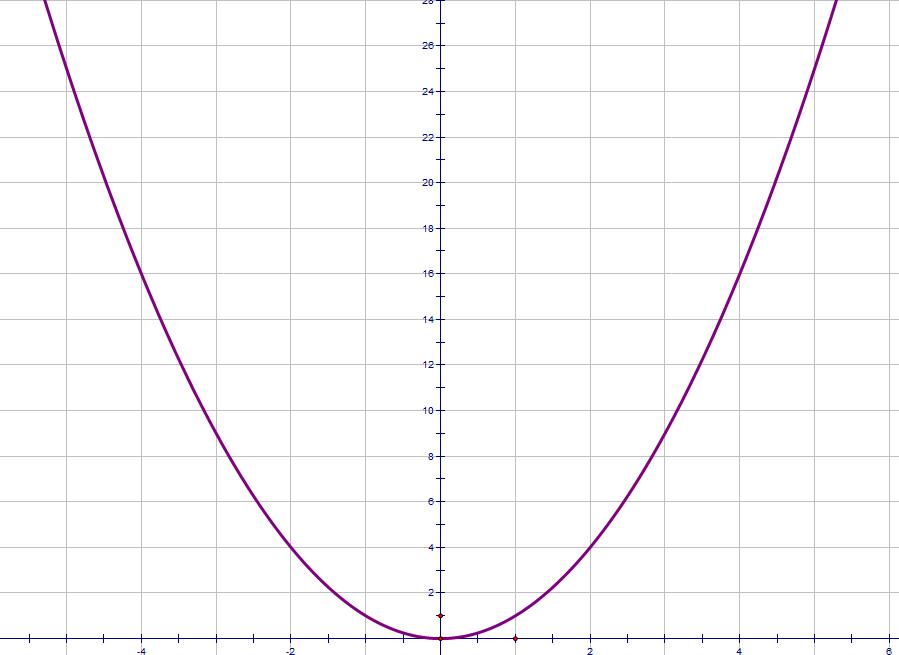
I won't write much about quadratic graphs. The shape is always the same - sometimes it's stretched a bit, sometimes it's upside down. The shape is called a parabola
There are three main ways of writing quadratic functions: ax2 + bx + c (expanded); a(x + b)2 + c (completed square); (ax + b)(cx + d) (factorised). Each has its own advantages when it comes to drawing the graphs as shown in this table.
| Example | Advantage | Graph |
|---|---|---|
| x2 + 4x + 8 | Easy to find y-intercept Here it's (0, 8) |
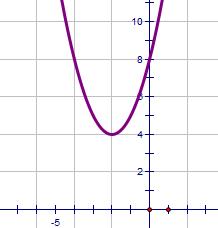 |
| (x + 2)2 + 3 | Easy to find max/min coordinates Here it's (-2, 3) |
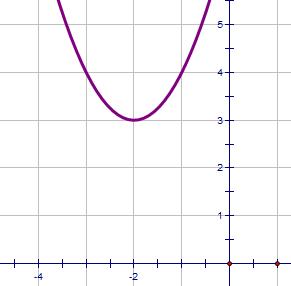 |
| (x + 2)(x - 1) | Easy to find x-intercept. Here they're (-2, 0) and (1, 0) |
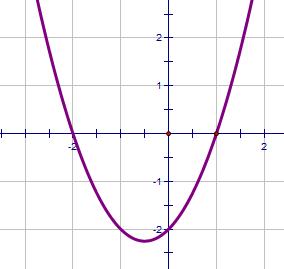 |
If the coefficient of x2 is positive, we get the U-shape. If it's negative, the graph is upside-down.
There's more about graphs in the Transformations of Graphs section.
The Discriminant
There are three main ways to solve quadratic equations. The easiest way is factorisation (see the table in the Quadratic Graphs section which shows the advantage of factorised quadratics). Unfortunately, this method is only available when the numbers are nice.
The second method is completing the square and from this comes the third: the quadratic formula.
The "b2 - 4ac" bit that we take the square-root of is called the discriminant. Notice that we get 2 solutions: one when we add the square-root and one when we subtract it.
But this only works if the discriminant is positive.
If it's zero then adding or subtracting doesn't make any difference so there is only one solution. If it's negative then we can't even take the square-root and so there are no solutions. This is summarised in this table.
| Equation | Discriminant | Graph | Roots | |
|---|---|---|---|---|
| x2 + 3x + 2 = 0 | b2 - 4ac = 1 | Positive | 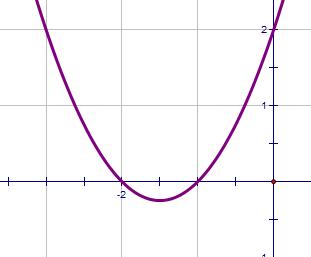 |
2 |
| 4x2 + 4x + 1 = 0 | b2 - 4ac = 0 | Zero | 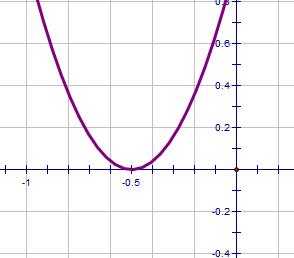 |
1 |
| 2x2 + 4x + 8 = 0 | b2 - 4ac = -48 | Negative | 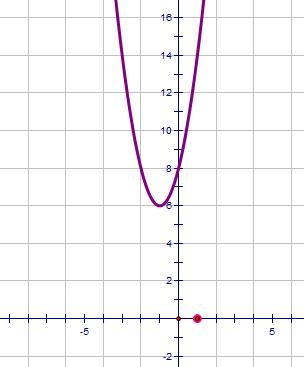 |
0 |
Loads of exams have questions involving the discriminant. Look through a few and you'll see. They all look a bit like the one in the video below (question from C1 May 2006)
Quadratic Equations
There are three ways to solve quadratic equations: factorisation, completing the square and using the formula.
When the numbers look nice you should always try to factorise first because it's the easiest method. If you find factorisation difficult then it's worth spending time practising your technique as it is very important that you can solve quadratic equations both quickly and efficiently.
Whenever you find factorisation too difficult (such as when the coefficient of x2 is not one) you can either complete the square or use the formula - the formula comes from completing the square - but do not use a machine. You should leave your answers as precise numbers (this means using surds rather than decimal approximations).
Simultaneous Equations
I like to call simultaneous equations simple-taneous equations because they are so simple! At this level they are always the same: one equation will be linear, the other quadratic. The technique for solution is...
- Make whichever variable (usually x or y) will make it easier, the subject of the linear equation.
- Substitute into the quadratic equation.
- Solve the quadratic equation to get (usually) two solutions.
- Don't forget to find the values of the other variable by using the linear equation.
- Write your solutions in pairs - make it clear which x value goes with which y value.
Inequalities
Inequalities at this level will be quadratic. The solution is straightforward, provided that you can solve quadratic equations and draw a quadratic graph.
- Write the inequality as ax2 + bx + c > 0 or < 0 or whatever it is.
- Solve the equation ax2 + bx + c = 0. This tells you when the curve goes through the x-axis. These values (there are usually two) are called critical values.
- Draw the curve y = ax2 + bx + c using the values you have just found.
- Highlight when the graph is positive (if your inequality is ax2 + bx + c > 0) or negative (if your inequality is ax2 + bx + c < 0)
- Write down the answer from your sketch.
A 4-mark question from C1 May 2006:
Find the set of values of x for which x2 - 7x - 18 > 0.
The solution, using Yarnell's method, is in the clip.
Polynomials
Poly-nomial means many-terms. ax2 + bx + c is a polynomial as it has three terms. Polynomials are named after the highest power that is involved, so ax2 + bx + c is a quadratic, whereas 2x3 + 4x + 9 is a cubic.
It is cubics that we will meet mostly at this level.
Expanding and Factorising
To expand three brackets, just multiply the first two together and then multiply the result by the third bracket.
Factorising cubics is a lot harder than factorising quadratics. For this reason we will only meet simple ones at this level. What I mean by that is that there will always be a really obvious factor (usually x).
eg Factorise x3 + 4x2 + 3x.
Each term has a common factor of x so simply take this out to leave x(x2 + 4x + 3) and than factorise the quadratic to get x(x + 3)(x + 1). Easy as.
Have a go at this (from C1 May 2006). The solution is in the clip.
Given that f(x) = (x2 - 6x)(x - 2) + 3x,
- express f(x) in the form x(ax2 + bx + c), where a, b and c are constants
- Hence factorise f(x) completely.
- Sketch the graph of y = f(x), showing the coordinates of each point at which the graph meets the axes.
Graphs of Functions
Along with quadratics you also need to know some other graphs. You should be familiar with straight-line graphs from GCSE and a couple of others. These are cubics and reciprocals.
Important Types of Graph
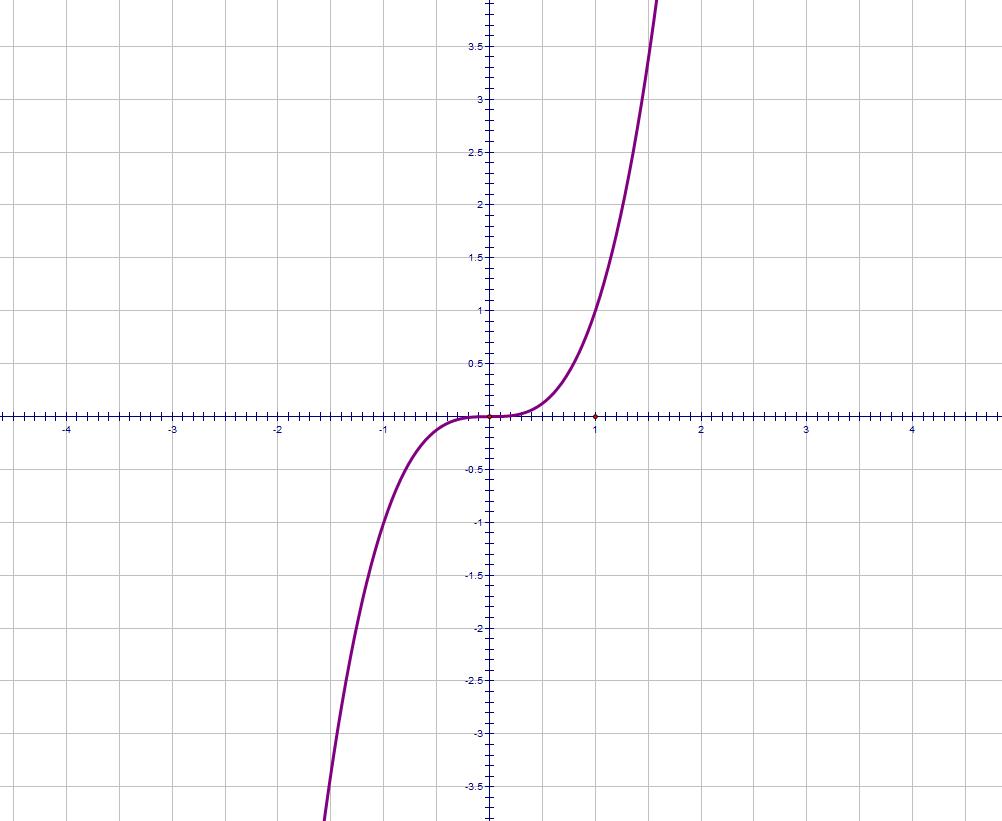
Here is a graph of y = x3
If the cubic is factorised then it is fairly easy to draw the curve. For instance, let's look at the graph of y = x(x - 2)(x + 3).
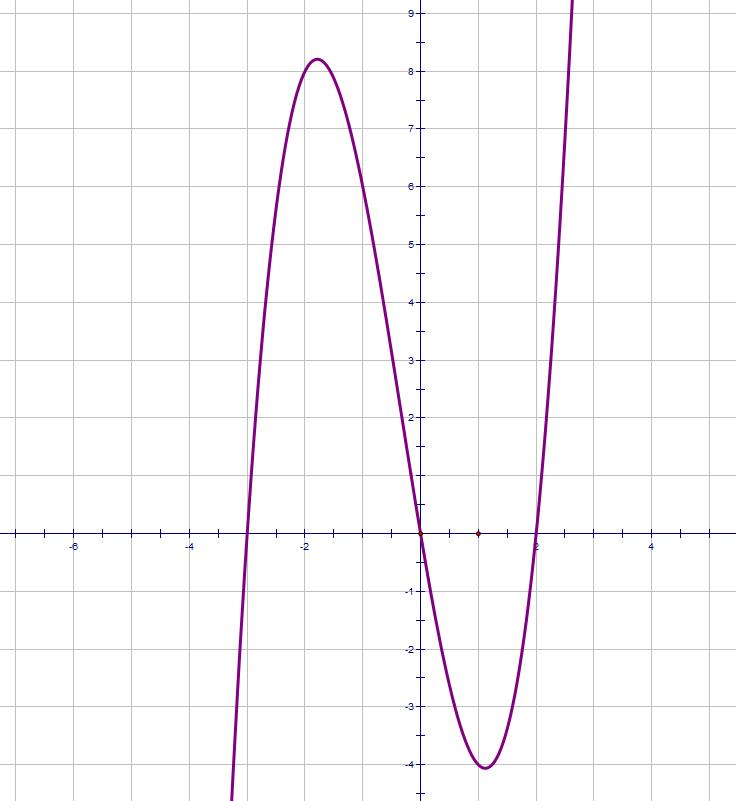
The graph goes through the x-axis when x=0, x=2, x=-3.
As the coefficient of x3 is positive (imagine multiplying the brackets - the x terms are all positive and so multiply together to be positive) the curve is a "right-way-up" cubic.
Notice where the curve passes through the axis.
And this is a reciprocal graph y = 1/x.
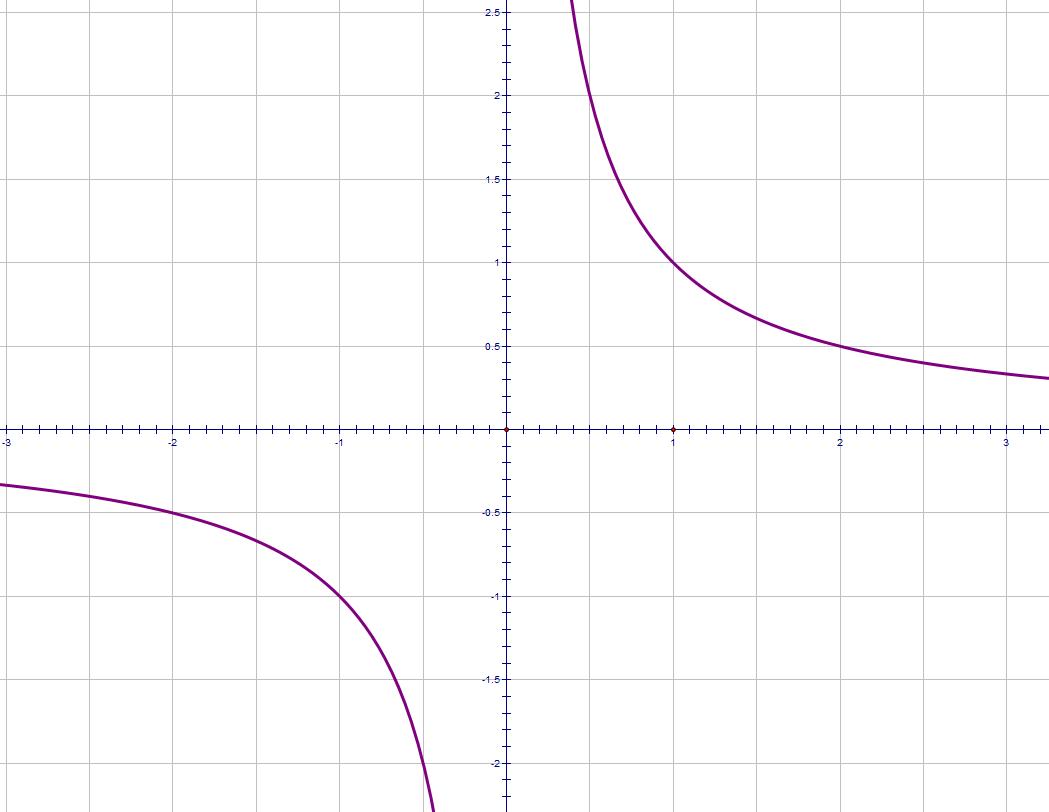
You should know how to draw these curves as you may be required to draw other versions of them formed by transforming them.
Transformations of Graphs
There are four transformations of graphs that you need to know.