C2

Sequences and Series

---

C2: Sequences and Series

---

Arithmetic sequences are all well and good but there are more important sequences.

One such sequence is where the terms multiply by a certain number each time like what happens with compound interest. These sequences are called geometric sequences.

Geometric Series

Remember that a sequence is an ordered list, a series is when we add them as we go. A sequence is geometric if the list multiplies as we go. The following are all geometric sequences.

eg 1, 2, 4, 8, 16,... multiplies by 2 each time

eg 5, 15, 45, 135,... multiplies by 3 each time

eg 3, -3, 3, -3, 3,... multiplies by -1 each time

eg 48, 36, 27, 20¼,... multiplies by ¾ each time

It is usual to label the first term a and the number that the list multiplies by each time, r for ratio.

General Term of a Geometric Series

So, if the first term of a geometric sequence is a, what's the second? (remember that the sequence multiplies by r each time).

That's right, ar.

And the third? We need to multiply the second term by r so it's ar².

The fourth? Yep, it's ar³

Here's a table...

Term	1st	2nd	3rd	4th	5th	6th
Value	a	ar	ar2	ar3	ar4	ar5

Notice that to get to the 6th term, we only need to multiply by r 5 times.

In general the n-th term is... u_n = ar^n-1

eg. In the geometric sequence with first term 9 and ratio 2, find the 11th term

Answer... u₁₁ = ar¹⁰

= 9×2¹⁰ = 9216.

Sum of Terms

Now let's look at the sum of the first n terms in a geometric series.

S_n = a + ar + ar² + ar³ + ... + ar^n-1

The clever trick we're going to use is (and you need to know this) to write the same sum below, only this time we multiply everything by r.

Sn =	a +	ar +	ar2 +	... +	arn-1
rSn =	ar +	ar2 +	ar3 +	... +	arn

So what? You said this was meant to be clever...

Here's the clever bit. Move the bottom row along a bit to line the similar tems up.

Sn =	a +	ar +	ar2 +	... +	arn-1
rSn =		ar +	ar2 +	... +	arn-1 +	arn

Now subtract the bottom row from the top one. All terms cancel except the a on the top and the arⁿ on the bottom.

So the result is:

S_n - rS_n = a - arⁿ.

Factorising:

S_n(1 - r) = a(1 - rⁿ)

And so:

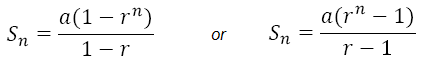
The first of these two is obviously from the equation above it. The second comes from subracting the top equation from the bottom and doing everything else the same.

We use the first when r < 1, and the second when r > 1. This way we avoid negative demoninators.

Clever eh?

Sum To Infinity

There's an old puzzle about a worm 1 metre down a well. Every day it crawls up a bit. In the first day it crawls ½ a metre. In the second day it crawls up ¼ metre. And so on, each day crawling half what it did the day before. The question is: how long before the worm reaches the top?

Try to find the answer to this before moving on; you'll get a feel for what's coming.

After day 1, the worm still has 1/2 m to go. After day 2 he has climed 1/4 metre, leaving 1/4 metre left. After day 3 he climbs 1/8 metre and still has 1/8 metre to go. You can quickly see that, although he is getting ever closer to the top, he never reaches it. It's as if the top is an asymptote.

The worm puzzle can be answered using the sum of a geometric series.

Here the ratio is ½ and the first term is ½. Using

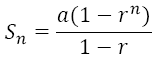
Substituting values we get

1 = ½(1 - ½ⁿ) / (1 - ½)

Sorting all this out (and I can't be bothered here - do it on paper) we end up with

½ⁿ = 0

But, as we know for the graph of >a^x this can never happen. Not in a million years.

So what to do? Here's a problem similar to the one we first met in differentiation. In the limit the sum has a final answer.

If the ratio is between -1 and 1 then the terms get closer and closer to zero the further we go. This means that they have a limit. The rⁿ bit will approach zero as n gets larger. In the limit it equals zero. This means that the formula becomes...

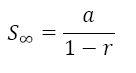
Where S_∞ is pronounced "sum to infinity".

eg. Find the sum to infinity of the geometric series 12 + 3 + 3/4 + 3/16, ...

Each term is ¼ the previous one. So a = 12 and r = ¼. As r is less than one we can find a sum to infinity.

S_∞ = a / (1 - r)

= 12 / (1 - ¼)

= 12 / ¾

= 16.

I just checked three random C2 exam papers and every one contained a geometric series question involving finding the sum to infinity. Here's two of them.

---

Binomial Expansions For Integer Powers

Grab a calculating machine and work out what these are: 11², 11³, 11⁴.

Notice anything? We'll come back to this.

Grab some playing cards (or anything that has 2 different sides - right way up and wrong way up - coins will do but it isn't so easy to see).

Take 2 of your cards and place them next to each other. There are 3 different possibilites here: both the right way up, one the right way up, none the right way up. But there are 2 different ways of arranging the cards to have one the right way up.

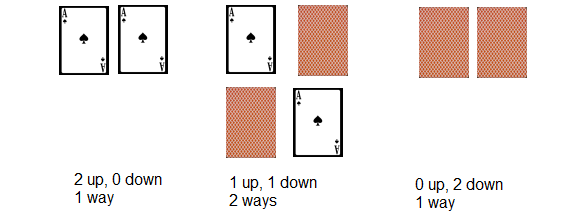
Now take three cards. This time there are 4 possibilities. How many of each are there?

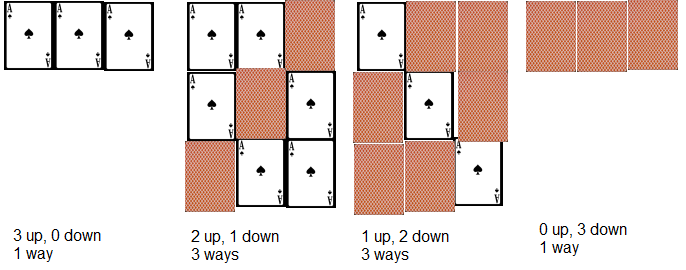
Have a go at the same thing with four cards.

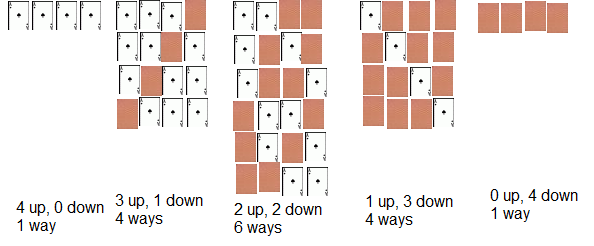
Notice anything? We'll come back to this.

The Binomial Theorem

Right, now for some algebra. Grab a pen and expand (x + y)². Write your answer in ascending powers of x.

You should have got (x + y)² = x² + 2xy + y².

Another way of writing this is 1x²y⁰ + 2x¹y¹ + 1x⁰y².

Daft as this looks, have a go at expanding (x + y)³ in the same way.

Finally, have an expand of (x + y)⁴.

Notice anything? Watch this...

If that was a bit confusing, don't fret. The main thing that you need to know is how to find the coefficients. There are three ways.

1. Pascal's Triangle. The best method if the power is small
2. The ⁿC_r button. The best method for large powers
3. The formula method. The only method when the power is unknown

Let's see this at work in a couple of exam questions. Thankfully binomial expansion questions are always easy and come in two flavours as you'll see in the clips.

Sorry about the clip's end. I'll add an exam question of this type when I find one.