Trigonometry
Trigonometric Rules
We'll start by having a look at a couple of things from GCSE.
The Sine Rule
Right, straight into a clip of this.
The Cosine Rule
Cosine Rule is just like Pythagoras' Theorem, only with a bit of an adjustment on the end. Here's a clip to show where the rule comes from.
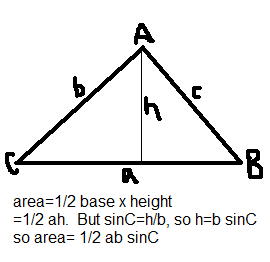
Area of a Triangle
Radian Measure
How tall are you?
Some people answer that question in centimetres, others in feet and inches. The fact is that we can use either and it is possible to convert from one to the other.
It's the same with angles. Sometimes it's more convenient to use radians than degrees. Sometimes it is vital to use radians (such as in C3 calculus)
Have a look at this clip. Ignore the bit after about 7 mins where he goes on about angular velocity or summat
In the clip the fella explains that (provided everything is in radians) we can find some calculations very straightforward.
Arc Length
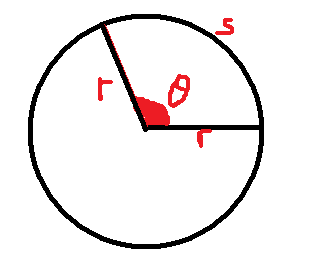
If the angle, θ is measured in radians, then the arc length, s, is simple to find.
The whole circumference has length C = 2πr. We only need a fraction of this. The fraction we need is θ÷2π, so the arc length is found thus:
s = θ/2π × 2πr
s = rθ
Area of Sector
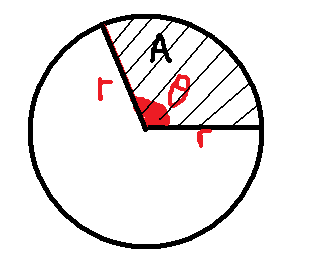
If the angle, θ is measured in radians, then the area of the sector, A, is simple to find.
The whole circle has area = πr2. We only need a fraction of this. The fraction we need is θ÷2π, so the area of the sector is found thus:
A = θ/2π × πr2
A = ½r2θ
Trigonometric Functions
Right, time for some hard work. At GCSE you were probably taught that the sine of an angle was calculated by dividing the opposite side's length by that of the hypotenuse.
There is something wrong though. Firstly, what if there is no right angled triangle? Can we have a sine of an angle if it's not part of a right angled triangle? Look at what we've already used in the sine and cosine rule to answer this. It looks as if we can find the sine of an angle without even considering a right-angled triangle.
Also, we use trigonometry in the Cosine Rule for angles which are greater than 90°. What can this possibly mean?
Fact is, we need to rethink what trigonometric functions are. Notice that I wrote functions in italics. At GCSE sine, cosine and tangent are thought of as ratios or fractions. But most people are happy to call them functions without stopping to think about what this means.
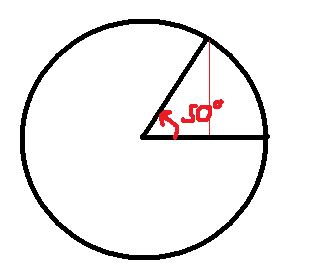
Back to the circle. We are going to measure all angles counter-clockwise from the positive x-axis. So, this angle is about 50°.
Notice where the angle starts from (the x-axis) and which way it's measured (counter-clockwise)
Now imagine the circle has a radius of one and is drawn on axes, centred at (0, 0). The side opposite our angle is the sine of the angle (because the hypotenuse is 1) and the side adjacent to our angle is the cosine of the angle.
In this case opposite is the same as the y-coordinate and adjacent is the same as the x-coordinate.
You should be able to find two angles where the cosine (x-coordinate) is about ½
Graphs of Trigonometric Functions
If you bear in mind that the sine of an angle is the y-coordinate, then imagine what happens as we increase the angle round the circle.
Open up the file in the last section if it helps. Drag the point around and watch what happens to the sine. It increases quickly at first but then slows down before reaching the highest point at 1. Then it comes down, slowly at first before gaining speed. It becomes negative when the angle goes beyond 180° and reaches a mimimum possible value at -1.
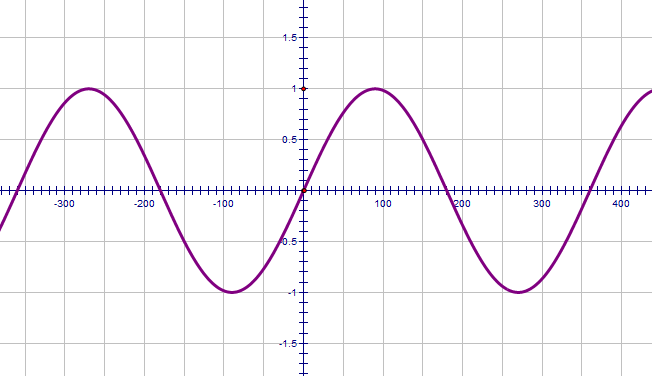
This is the sine curve. Notice that it starts at zero (the y-coordinate at zero is zero) and reaches a maximum value at 90°.
It repeats every 360° like you'd imagine.
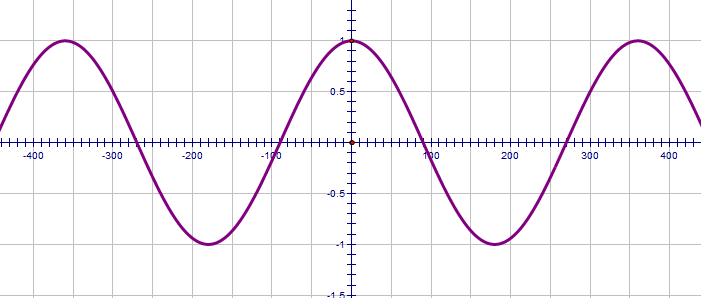
The cosine curve is the same as the sine only it is translated by 90°.
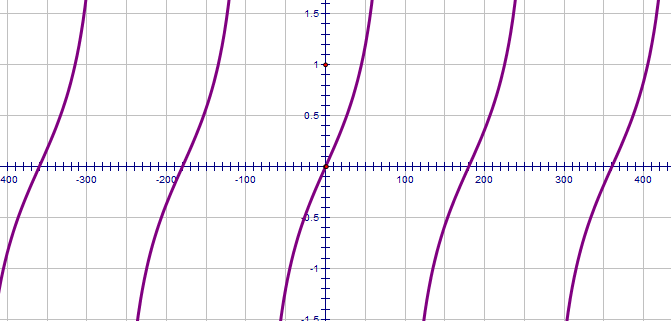
We haven't discussed tangent much. I'll add a java-thing later. For the time being, notice that it repeats every 180°:.
Trigonometric Identities
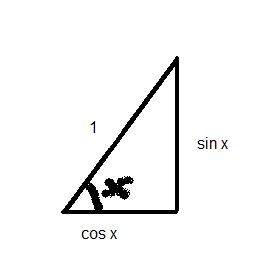
Thinking back to the definition of sine and cosine.
Remember, in a circle with radius one, the opposite (y-coordinate) is the sine of the angle, the adjacent is the cosine
From Pythagoras' Theorem, one thing should be obvious here. We don't need any fancy algebra.
sin2θ + cos2θ ≡ 1
If you haven't seen that "≡" sign before then I'll tell you that it means "is identical to".
The difference between "equal to" and "identical to" is that "=" is used when there are certain values to find or solve. "≡" is used when the statement is true no matter what values are substituted.
So x + 2 = 5, is an equation. We can try to solve it.
And x + x ≡ 2x is an identity. There is no point trying to solve it - it's always true.
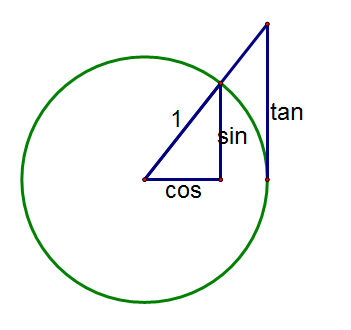
Now draw a tangent to the circle on the right. Extend the angle beyond the circle until it hits the tangent. The y-coordinate of this intersection is called the tangent of the angle.
Notice that at 0° the tangent is zero, whilst at 90° the angle is parallel to the tangent from the circle and so they never coincide. After 90° it becomes negative.
So that's why it's called the tangent!
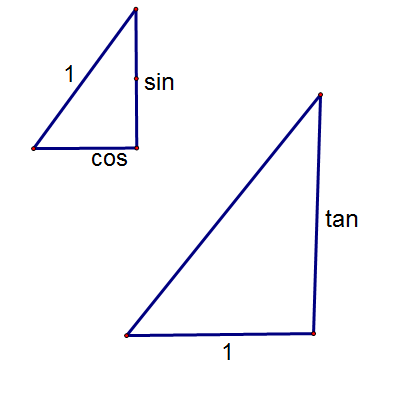
In this diagram there are two similar triangles. Why? They have the same angles, that's why.
"Hold on there," I here you say, "where did that '1' come from in the larger triangle?"
I'll leave it to you to answer that question.
Now given that they're similar triangles, the ratios sine:cosine and tangent:1 must be the same.
In other words sinθ ÷ cosθ ≡ tanθ...
Trigonometric Equations
There are two types of trig equations, both of which are in the poor-quality clip below.
The first type involves using identities from above. Look out for either of these
- sin2θ and cosθ in the same equation
- tanθ will definitely involve using the other identity
The second involves finding all the solutions in a certain range. eg.
Find all solutions 0<θ<360 of sin(2θ + 30) = 0.5
- Change the range 0<θ<360 so 30<2θ+30<750. These numbers came from 2×0+30 and 2×360+30
- Solve: 2θ + 30 = 30, 150, 390, 510, 750. Reject 30 and 750 as out of range
- Subtract 30 and divide by 2. θ = 60, 180, 240