D2

Critical Path Analysis

---

A

---

Imagine that you are making a lovely cup of tea. We could break the process down into several jobs or activities, some of which depend on others to have finished before they can start.

The activities each need one person to do them. No-one can do two things at once. Here is a list of all the jobs:

Clean cup, boil water, put bag in cup, pour water into cup, add sugar, add milk, drink tea.

The problem is that you can't pour water into a dirty cup. You must clean the cup before pouring in the water. We can summarise the order in which we do the activities in a precedence table.

Activity	Depends On
Clean cup (A)	-
Boil water (B)	-
Put bag in cup (C)	A
Put water into cup (D)	B, C
Add sugar (E)	A
Remove bag (F)	D
Add milk (G)	F
Drink tea (H)	E, G

From this we can draw a graph or activity network.

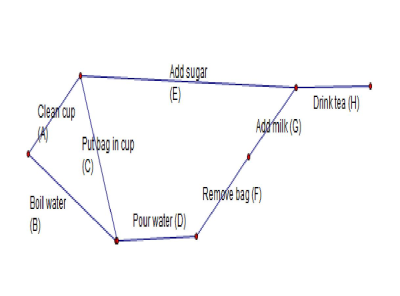
I really should've put arrows on the edges, but I can't be bothered. This network shows that you can add the sugar at any time before drinking provided you have a clean cup.

The branch of mathematics called Critical Path Analysis is all about getting this job done in the shortest time possible. Now I know that it only takes one person to make a cup of tea, and that you can be cleaning a cup whilst the water is boiling, but just for now pretend that you have to power the kettle by running on a treadmill or something, so that you're fully occupied whilst the water heats up.

Hopefully it is clear that if one person is cleaning a cup, another could be boiling the water at the same time, thus speeding up the process. Let us now put some times for the activities (this is not meant to be realistic!)

If we have as many workmen as possible, how quickly can we make and drink our tea?

We start the clock at zero. Alan cleans a cup whilst Bob boils the water. There is no point having anyone else at this point as there is nothing else to do. After 3 mins the cup is clean and Alan can now start to put the bag in the cup. After 5 mins he has finished this and can now add the sugar. After 8 mins the water has boiled and Bob can now pour the water into the cup ( taking care not to scold Alan). After 10 mins Bob can remove the bag and Alan has finished adding the sugar. Either workman can now add the milk and, after 15 mins, the tea can be drunk. The job is complete after 20 mins.

Imagine that you are Alan in this example. You should notice that you don't need to rush to add the sugar because you'll only end up having to wait for Bob to do his jobs before the tea is ready.

Also notice that Alan doesn't have to start cleaning the cup immediately. Alan's first two jobs (clean cup, put bag in cup) only take a total of 5 mins, whereas Bob takes 8 mins just to boil the water. This means that Alan can give Bob a 3 minute head start and still not slow the project down.

Now look at it from Bob's point of view.

If they are to get this cuppa made and drunk as quickly as possible then Bob can't hang around at all. If he delays any of his jobs then the whole project is slowed down.

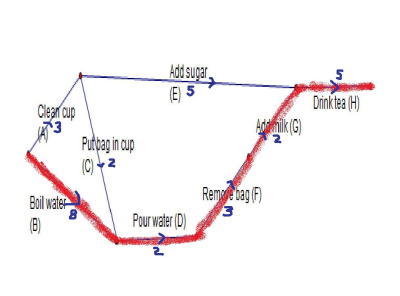
Bob's jobs are shown in red. Alan's are the others. In total the job takes 20 minutes and poor Bob works flat out for the whole project whilst Alan can take it easy.

Because the whole project is determined by the red jobs starting on time, they are called critical activities. The red route (or path) from start to finish is called the critical path.

---

Algorithm For The Critical Path

We will now look at the algorithm for finding the critical path.

The nodes on the activity networks denote events. An event in this case just means that all jobs leading into the vertex have been done. So the node with "clean cup" leading into it stands for the time when the cup is clean. The node with B (boil water) and C (put bag in cup) feeding into it stands for the time when we have done both of these activities and are ready to do D (pour water).

Each node has a number. The beginning node is labelled "0". After this, the next node that we label is the one with just A leading into it. This node is labelled "1".

Now, the next node to label is the one with C and B leading into it. Label this "2". Can you see why the labelling must be in this order?

It is illogical to label the node which B leads into before the one that A leads into. The reason is that we must have arrived at the node we labelled "1" before the one we labelled "2" if we think about what the nodes mean. Our "1" represents the event of having a clean cup whilst our "2" represents the event of having a bag in the cup and boiling water - ready to pour the water. Logically, this event must come after our event "1".

Label all the vertices in the logical order.

We now go through the graph finding the earliest possible times when we can be at the vertex. Remember that the vertex "2" represents having done both B and C, so we cannot be at "2" in only 5 minutes - it takes 8 minutes at least to be ready to pour the water.

Watch this clip which explains the process of finding the critical path.

Use of Dummies

Try to form a network from this information.

Activity	Depends on
Clean cup ()A)	-
Boil water (B)	-
Put bag in cup (C)	A
Pour water in cup (D)	B, A

Hopefully you see the difficulty. There is no way of connectiong C and D to the right bits. If you connect A and B together at node 1 then you cannot show that C depends only on A and not on B. We need a way around this.

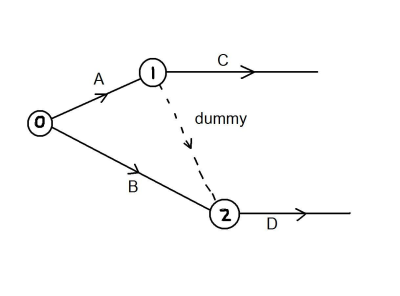
To connect C in the above example is easily done. The problem now is to show Ds dependence on both B and A.

To do this we use a dummy. A dummy is a dotted line with zero weight that is needed to show the right connections. The above activities can now be represented like this.

You can have as many dummies as you need in one of these networks. The exam question below is from Jan 2005. Have a go first then check the solution.

The precedence table for activities involved in producing a computer game is shown below.

Activity	Must be preceded by
A	-
B	-
C	B
D	A, C
E	A
F	E
G	E
H	G
I	D, F
J	G, I
K	G, I
L	H, K

An activity on arc network is to be drawn to model this production process.

1. Explain why it is necessary to use at least two dummies when drawing the activity network.
2. Draw the activity network using exactly two dummies.

Gantt (Cascade) Charts

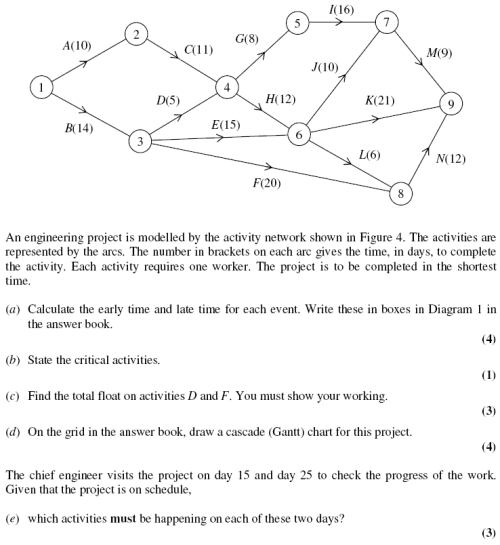
To explain how Gantt Charts are used, I'll dive straight into an exam question.

This is from May 2006

I have just realised that I have already done a clip for the first bit so I will pick up where that clip left off...