C1: Differentiation
Congratulations! you have chosen to learn about the single greatest mathematical invention of the last thousand years!
Calculus is made up of two main parts: Differentiation and the next section, Integration.
A Brief History of Calculus
Taking mathematics from the beginning of the world to the time of Newton, what he has done is much the better half.
.
Ask any one what happenned in England in 1665-1666 and they'll tell you. The Great Plague killed 20% of the population of London and the Great Fire burned 13,000 houses and nearly a hundred churches in the City.
Nice times.
At this time, a 24-year-old mathematics graduate named Isaac Newton left Cambridge University to escape the plague. It was during this time that the greatest period of mathematical discovery ever reported happened.
Newton's Great Discoveries
During his time away from Cambridge in 1665-1666, Newton discovered four amazing things, any one of which would have made him a household name. He discovered
-
the nature of colours:
- Newton discovered that white light was made up of all the colours of the rainbow. He discovered that the primary colours, which all light is made from, are red, green and blue. This discovery was made when he was working on optics and used an imperfect lens in his refracting telescope. He cured this by inventing the reflecting telescope with a mirror replacing the lens.
- the law of Universal Gravitation
- Newton claimed that it was the very same force that attracted falling apples to earth that kept the earth in orbit around the sun. Furthermore he claimed that the earth pulls the sun with exactly the same force as the sun pulls the earth. And he solved the equations to prove it .
- the binomial theorem
- The binomial expansions had been known about for over 50 years, but it took Newton to extend the theory to non-integer powers. This opened up a whole new world of analysis
- the calculus
- Newton's greatest mathematical discovery which today is a vital part in many modern disciplines including: physics, engineering, economics, statistics, medicine, demography, ... in fact anything where we are interested in knowing how one thing affects another.
What is Calculus?
As stated above, calculus is made up of two branches: differentiation and integration. Differentiation is all about finding rates of change, or to put it another way: how is one thing changing as another does. For example: how your speed changes as time passes is called your acceleration. How prices change from year-to-year is called inflation...
Thinking graphically, differentiation is all about finding gradients of curves.
Gradients of Tangents
It is usual to start by looking at y = x2 and that is what I do in this clip.
In the clip you see how we can use algebra to find the gradient at any point on the curve y = x2.
We are now in a position to find the derivative (gradient function) of many functions.
I won't go into detail but we can now differentiate any function of the form f(x) = ax n
Before I explain how to do this, let's first look at how we write all of this down...
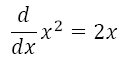
I like this way of writing our result from the clip. I read this as "The derivative of x2 is 2x"
There are other ways of saying this. They include
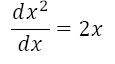
This is pretty much identical to the first way of writing it...
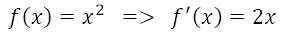
This one is read as "if f(x) = x2 then f primed of x = 2x. Some folk pronounce this as f dash... but a dash looks like this - and a prime looks like this '.

This is read as "dee why by dee eks" and means that we are differentiating y with respect to x. This confuses some people. Basically it means "what is happening to y as x increases.
If y = x2 then we cannot differentiate y with respect to t (not until C3 any way) because we have no way of knowing what happens to y as t increases, as y is not defined in terms of t.
Here is a summary of some simple functions and their derivatives. You should have a go at checking this using Excel, like I did in the clip.
| f (x) | f' (x) |
|---|---|
| x2 | 2x |
| x3 | 3x2 |
| x9 | 9x8 |
| 1/x (=x-1) | -x-2 (=-1/x2) |
| axn | anxn-1 |
A couple of pints to note:
- As we can write 5x as 5x1, its derivative is 5x0 but x0 = 1 so the derivative is just 5. This shouldn't come as a surprise when you think about the gradient of y = 5x. Of course, there's nothing special about 5; any number times x has the number as the derivative.
- As we can write 9 as 9x0, its derivative is 0x-1, which is just zero. Of course there's nothing special about 9; any number has zero as its derivative. This shouldn't come as a surprise when you consider the gradient of the graph y = 9.
One last point: these are the only functions that we can differentiate in C1 and C2. They all can be written as axn. To differentiate √x we must first re-write as x½
A Problem on the Horizon
But I leave hanging the problem that we have.
We are either left with a the gradient being somewhere between two values (2x minus something and 2x plus something) or, if we say that the something is zero, then we have divided by zero in our calculation.
Newton and Leibniz simply said that we can ignore the small value, often called δx, where "δ" means a small increment.
But this is not good enough.
The philosopher Bishop Berkeley wrote an essay on this called "A Discourse Addressed to an Infidel Mathematician", where he pointed out that even if the calculus led to correct conclusions, it doesn't make it a genuine science. He compared mathematicians' blind following of Leibniz/Newton with religion. I think it's even worse than that; if mathematicians couldn't resolve the problem then what would be the point of doing more maths?
Since Euclid's time, human beings had always valued mathematics for its rigorous nature. Without proof maths was devalued.
The Problem Gets A Solution
Thanks to Augustin Cauchy and Weierstrass the problem was fixed using the idea of limits. Both Newton and Leibniz had tried this over 150 years earlier but never really cracked it.
More recently, in the 1960s Abraham Robinson developed a branch of mathematics called non-standard analysis which brought mathematical rigour to infinite and infinitisimal (infinitely small) numbers.
Applications To Equations Of Lines
Now we'll have a look at how we can use what we have learned to find the equation of tangents and normals to a curve at a certain point.

The diagram shows the curve with equation y = x2 + 3x + 5.
Our task is to find the equations of the red and blue lines.
The red line is the tangent to the curve at (-1, 3)
The blue line is the normal at the same point. Those of you studying Mechanics will know that the normal reaction is always at right anles to the point of contact - this is because normal means perpendicular.
Remember how to find the equation of a straight line given a point and the gradient?
Well, we know the point is (-1, 3), so all we need is the gradient. But it's a curve I hear you say. How can we find the gradient of a curve?
That's where differentiation comes in.
If y = x2 + 3x + 5, then y' = 2x + 3. We know that the x-coordinate of our point is -1, so the gradient must be 2(-1) + 3 which is 1. This tells us that the gradient of the normal is -1 as the gradients must multiply to make -1.
So this question is now easy. The gradient is 1 and the point is (-1,3).
Using y = mx + c, substituting m = 1, x = -1 and y = 3 gives
3 = 1(-1) + c
and so c = 4 and the equation of the tangent is y = x + 4.
For the normal we just do the same only m = -1. Its equation is y = -x + 2.
To finish, here's a slightly trickier question what I jacked from the Edexcel specification book.
