C2: Coordinate Geometry in the (x, y) Plane
If Coordinate Geometry in C1 was all about finding the equation of a straight line, then the same section in C2 is all about finding the equation of a circle.
Before we have a look at this, let's remind ourselves of a few GCSE facts.
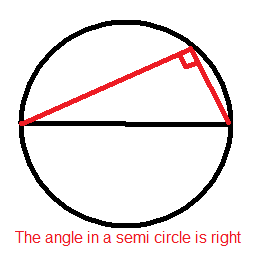
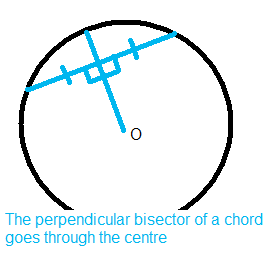
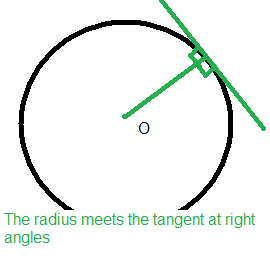
Equation of a Circle
Just like the equation of a straight line, there are many ways to write the equation of a circle.
But one way is by far the best and easiest.
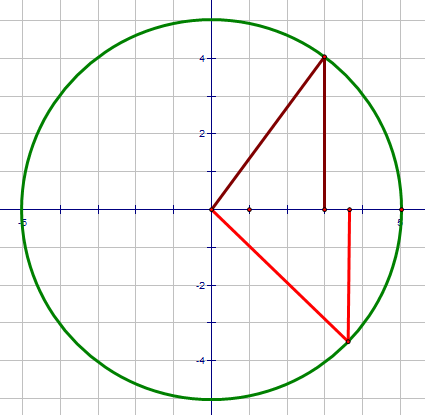
The green circle is centred at (0, 0) and has radius of 5.
Applying Pythagoras' Theorem to the brown triangle gives x2 + y2 = 52 because the radius of the circle and therefore the hypotenuse of the triangle equal 5.
Applying the theorem to the red triangle gives the same result.
In fact, all points on the circle satisfy the same equation: x2 + y2 = 52, and so this is the equation of the circle.
Notice that I didn't work out what 52 is. It's best left as it is.
The equation of a circle, radius r, centred at (0, 0) is x2 + y2 = r2
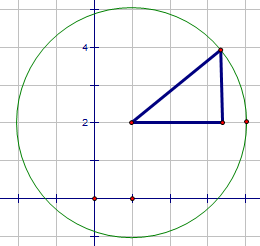
This circle has a radius of 3 and is centred at (1, 2).
Writing Pythagoras' Theorem for the blue triangle: the horizontal distance is (x - 1) and the vertical distance is (y - 2).
This gives us the equation as (x - 1)2 + (y - 2)2 = 32.
In general: the equation of a circle, centred at (a, b) with radius r is...
(x - a)2 + (y - b)2 = r2.
Of course we could multiply out those brackets but then we'd lose the simplicity of the equation.
eg. Find the equation of the circle centred at (4, -6) with radius 9.
Answer (x - 4)2 + (y + 6)2 = 92
eg. Find the centre and radius of the circle with equation x2 + 6x + y2 - 8y - 11 = 0
We need to complete the square for both x and y.
The x bit must be (x + 3)2, and the y bit must be (y - 4)2. Multiplying this lot out gives
x2 + 6x + y2 - 8y + 25.
The 25 comes from the 32 + 42.
We have ... + 25 when we need ... -11, so we must subtract 36 from our brackets to give
(x + 3)2 + (y - 4)2 = 36 (= 62)
So the circle has centre (-3, 4) and radius 6.
The video has three exam questions from Jan 2009, May 2006 and Jan 2005.
Get hold of these papers and have a go at the circle questions before playing the clip.
