C2: Differentiation
C1 introduced differential calculus. We will now look at a key use: finding maxima and minima.
The Second Derivative
If you thought that differentiating once was great, you're going to love differentiating twice!
But why would we want to do that? Well if the first derivative dy/dx represents the rate of change of y with respect to x, which is the gradient of the curve y = f (x), the second derivative d2y/dx2 represents the rate of change of the gradient.
So, by differentiating twice we can tell whether the gradient is increasing or decreasing. But why would we be interested in that? Answer to that is coming up soon.
As suggested above, the notation for the second derivative follows from the first.
If the first derivative is written dy/dx then the second is written d2y/dx2 and is pronounced dee-two-why-by-dee-eks-squared. Some folk are confused as to why the "square" goes with the "d" and not the "y". Think of the symbol as d2/dx2. This notation was Leibniz's prefered type.
If we want to differentiate x3 twice, there's nothing wrong with writing it as d2x3/dx2, apart from the fact that it looks a bit weird.
If we use Joseph Legrange's notation, the first and second derivative are written as f '(x) and f ''(x) respectively. Or we could use y' and y'' (pronounced "double primed")
Newton developed differentiation with mechanics in mind. For this reason he was mostly interested in what happened to something with respect to time. So Newton would be more interested in the rate of change of velocity with respect to time (this is called acceleration). For short he'd write v with a dot on it (HTML doesn't provide such a symbol and I can't be bothered finding a way round this, so I will avoid Newton's notation)
eg: If y = 3x2, find y''.
Answer: y' = 6x, so y'' = 6.
Stationary Points
Now we get to the point of the second derivative. Finding maxima/minima.
Have a look at the graph of y = 1/x + x3
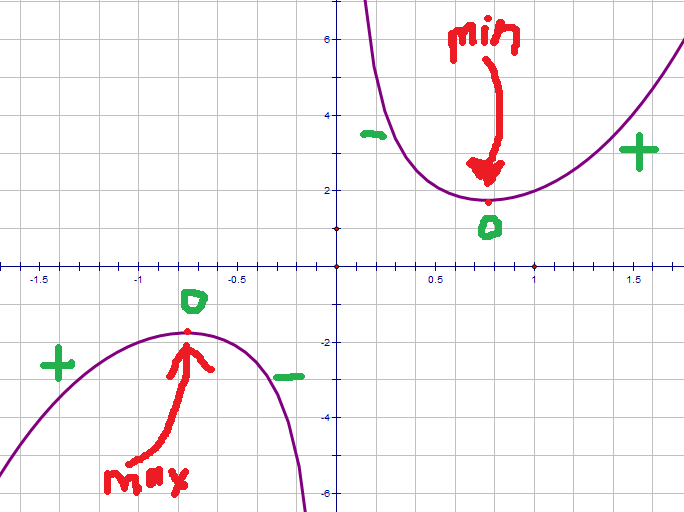
I have marked (in red) two interesting points. One is a maximum point, the other is a minimum point. Notice that the so-called maximum point is certainly not the maximum possible value; indeed the minimum is larger than the maximum!
When we talk about maxima and minima, we usually mean local maxima/minima. This is when a function is bigger/smaller than all the other points in its neighbourhood.
In green I have added the sign of the gradient. At the maxima, the gradient goes from positive to negative. At the minima, the opposite happens. At BOTH maxima and minima the gradient is zero.
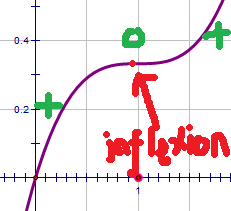
Points where the gradient is zero (such as maxima/minima) are called stationary points. In fact there are three flavours: maxima and minima we've seen, the other is called inflexion and isn't really very interesting. Inflexion looks like this.
Notice that at the point of inflexion, the gradient went from positive to zero, then went positive again.
Now, have a think about what is happening to the second derivative at each type of stationary point. The answer's in the text box...
This here table summarises the info...
| y' | y'' | |
|---|---|---|
| maxima | 0 | neg |
| minima | 0 | pos |
| inflexion | 0 | 0 |
In fact there are other forms of inflexion but they just aren't very interesting at the moment.
If Hell's Kitchen wasn't on, I'd do a clip or two at this point but there's no way I'm turning the telly off.
These questions are from the usual papers: Jan 2009, Jan 2005 and May 2006. Have a bash at the differentiation bits.
